|
|
@@ -15,7 +15,7 @@
|
|
|
> **转移概率(P)**:当执行某个动作后,当前状态会以某种概率转移到另一个状态;
|
|
|
> **奖赏函数(R)**:在状态转移的同时,环境给反馈给机器一个奖赏。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
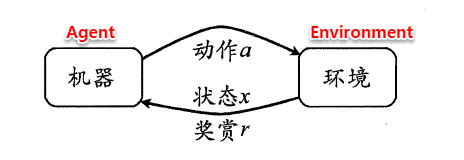
因此,**强化学习的主要任务就是通过在环境中不断地尝试,根据尝试获得的反馈信息调整策略,最终生成一个较好的策略π,机器根据这个策略便能知道在什么状态下应该执行什么动作**。常见的策略表示方法有以下两种:
|
|
|
|
|
|
@@ -24,7 +24,7 @@
|
|
|
|
|
|
**一个策略的优劣取决于长期执行这一策略后的累积奖赏**,换句话说:可以使用累积奖赏来评估策略的好坏,最优策略则表示在初始状态下一直执行该策略后,最后的累积奖赏值最高。长期累积奖赏通常使用下述两种计算方法:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**16.2 K摇摆赌博机**
|
|
|
|
|
|
@@ -41,14 +41,14 @@
|
|
|
|
|
|
**ε-贪心法基于一个概率来对探索和利用进行折中**,具体而言:在每次尝试时,以ε的概率进行探索,即以均匀概率随机选择一个动作;以1-ε的概率进行利用,即选择当前最优的动作。ε-贪心法只需记录每个动作的当前平均奖赏值与被选中的次数,便可以增量式更新。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
###**16.2.2 Softmax**
|
|
|
|
|
|
**Softmax算法则基于当前每个动作的平均奖赏值来对探索和利用进行折中,Softmax函数将一组值转化为一组概率**,值越大对应的概率也越高,因此当前平均奖赏值越高的动作被选中的几率也越大。Softmax函数如下所示:
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+
|
|
|
+
|
|
|
|
|
|
##**16.3 有模型学习**
|
|
|
|
|
|
@@ -63,43 +63,43 @@
|
|
|
|
|
|
根据累积奖赏的定义,我们可以引入T步累积奖赏与r折扣累积奖赏:
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+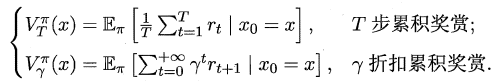
|
|
|
+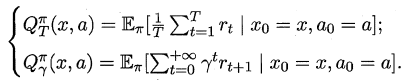
|
|
|
|
|
|
由于MDP具有马尔可夫性,即现在决定未来,将来和过去无关,我们很容易找到值函数的递归关系:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
类似地,对于r折扣累积奖赏可以得到:
|
|
|
|
|
|
-
|
|
|
+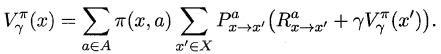
|
|
|
|
|
|
易知:**当模型已知时,策略的评估问题转化为一种动态规划问题**,即以填表格的形式自底向上,先求解每个状态的单步累积奖赏,再求解每个状态的两步累积奖赏,一直迭代逐步求解出每个状态的T步累积奖赏。算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
对于状态-动作值函数,只需通过简单的转化便可得到:
|
|
|
|
|
|
-
|
|
|
+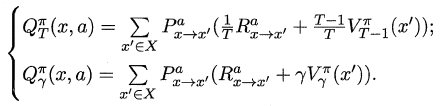
|
|
|
|
|
|
###**16.3.2 策略改进**
|
|
|
|
|
|
理想的策略应能使得每个状态的累积奖赏之和最大,简单来理解就是:不管处于什么状态,只要通过该策略执行动作,总能得到较好的结果。因此对于给定的某个策略,我们需要对其进行改进,从而得到**最优的值函数**。
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+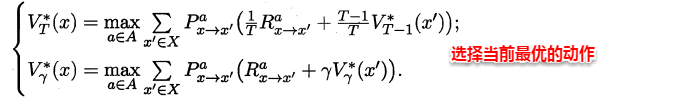
|
|
|
+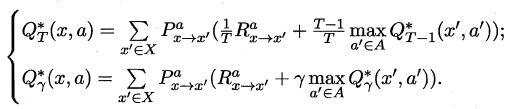
|
|
|
|
|
|
最优Bellman等式改进策略的方式为:**将策略选择的动作改为当前最优的动作**,而不是像之前那样对每种可能的动作进行求和。易知:选择当前最优动作相当于将所有的概率都赋给累积奖赏值最大的动作,因此每次改进都会使得值函数单调递增。
|
|
|
|
|
|
-
|
|
|
+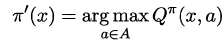
|
|
|
|
|
|
将策略评估与策略改进结合起来,我们便得到了生成最优策略的方法:先给定一个随机策略,现对该策略进行评估,然后再改进,接着再评估/改进一直到策略收敛、不再发生改变。这便是策略迭代算法,算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
可以看出:策略迭代法在每次改进策略后都要对策略进行重新评估,因此比较耗时。若从最优化值函数的角度出发,即先迭代得到最优的值函数,再来计算如何改变策略,这便是值迭代算法,算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**16.4 蒙特卡罗强化学习**
|
|
|
|
|
|
@@ -107,11 +107,11 @@
|
|
|
|
|
|
由于模型参数未知,状态值函数不能像之前那样进行全概率展开,从而运用动态规划法求解。一种直接的方法便是通过采样来对策略进行评估/估算其值函数,**蒙特卡罗强化学习正是基于采样来估计状态-动作值函数**:对采样轨迹中的每一对状态-动作,记录其后的奖赏值之和,作为该状态-动作的一次累积奖赏,通过多次采样后,使用累积奖赏的平均作为状态-动作值的估计,并**引入ε-贪心策略保证采样的多样性**。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
在上面的算法流程中,被评估和被改进的都是同一个策略,因此称为**同策略蒙特卡罗强化学习算法**。引入ε-贪心仅是为了便于采样评估,而在使用策略时并不需要ε-贪心,那能否仅在评估时使用ε-贪心策略,而在改进时使用原始策略呢?这便是**异策略蒙特卡罗强化学习算法**。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**16.5 AlphaGo原理浅析**
|
|
|
|
|
|
@@ -127,13 +127,13 @@
|
|
|
|
|
|
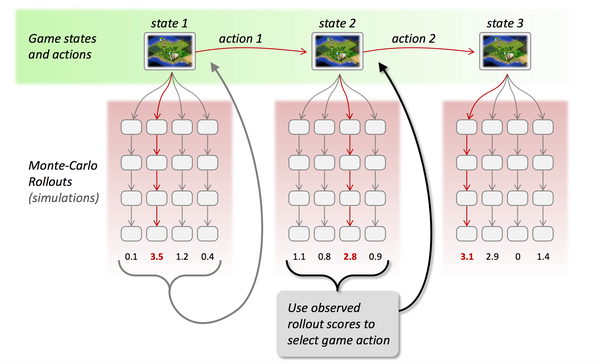
蒙特卡罗树是一种经典的搜索框架,它通过反复地采样模拟对局来探索状态空间。具体表现在:从当前状态开始,利用策略函数尽可能选择当前最优的动作,同时也引入随机性来减小估值错误带来的负面影响,从而模拟棋局运行,使得棋盘达到终局或一定步数后停止。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
> **3.强化学习(调整估值函数)**
|
|
|
|
|
|
在使用蒙特卡罗搜索树进行多次采样后,每次采样都会反馈后续的局面信息(利用局面函数进行评价),根据反馈回来的结果信息自动调整两个估值函数的参数,这便是强化学习的核心思想,最后基于改进后的策略函数选择出当前最优的落子动作。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
在此,强化学习就介绍完毕~同时也意味着大口小口地啃完了这个西瓜,十分记得去年双11之后立下这个Flag,现在回想起来,大半年的时间里在嚼瓜上还是花费了不少功夫。有人说:当你阐述的能让别人看懂才算是真的理解,有人说:在写的过程中能发现那些只看书发现不了的东西,自己最初的想法十分简单:当健忘症发作的时候,如果能看到之前按照自己思路写下的文字,回忆便会汹涌澎湃一些~
|
|
|
|