|
|
@@ -8,29 +8,29 @@
|
|
|
|
|
|
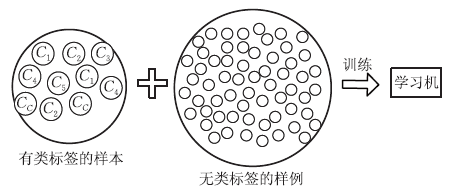
显然,**主动学习需要与外界进行交互/查询/打标,其本质上仍然属于一种监督学习**。事实上,无标记样本虽未包含标记信息,但它们与有标记样本一样都是从总体中独立同分布采样得到,因此**它们所包含的数据分布信息对学习器的训练大有裨益**。如何让学习过程不依赖外界的咨询交互,自动利用未标记样本所包含的分布信息的方法便是**半监督学习**(semi-supervised learning),**即训练集同时包含有标记样本数据和未标记样本数据**。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
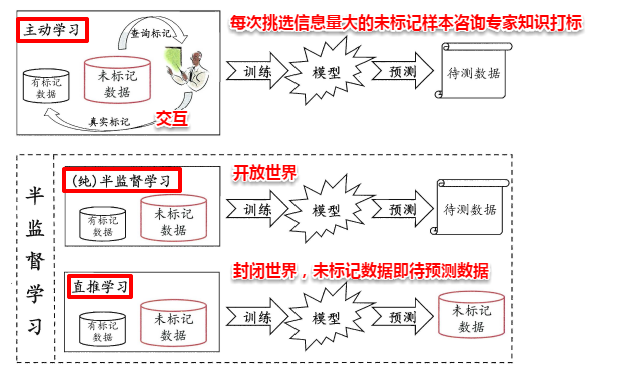
此外,半监督学习还可以进一步划分为**纯半监督学习**和**直推学习**,两者的区别在于:前者假定训练数据集中的未标记数据并非待预测数据,而后者假定学习过程中的未标记数据就是待预测数据。主动学习、纯半监督学习以及直推学习三者的概念如下图所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**14.1 生成式方法**
|
|
|
|
|
|
**生成式方法**(generative methods)是基于生成式模型的方法,即先对联合分布P(x,c)建模,从而进一步求解 P(c | x),**此类方法假定样本数据服从一个潜在的分布,因此需要充分可靠的先验知识**。例如:前面已经接触到的贝叶斯分类器与高斯混合聚类,都属于生成式模型。现假定总体是一个高斯混合分布,即由多个高斯分布组合形成,从而一个子高斯分布就代表一个类簇(类别)。高斯混合分布的概率密度函数如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
不失一般性,假设类簇与真实的类别按照顺序一一对应,即第i个类簇对应第i个高斯混合成分。与高斯混合聚类类似地,这里的主要任务也是估计出各个高斯混合成分的参数以及混合系数,不同的是:对于有标记样本,不再是可能属于每一个类簇,而是只能属于真实类标对应的特定类簇。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
直观上来看,**基于半监督的高斯混合模型有机地整合了贝叶斯分类器与高斯混合聚类的核心思想**,有效地利用了未标记样本数据隐含的分布信息,从而使得参数的估计更加准确。同样地,这里也要召唤出之前的EM大法进行求解,首先对各个高斯混合成分的参数及混合系数进行随机初始化,计算出各个PM(即γji,第i个样本属于j类,有标记样本则直接属于特定类),再最大化似然函数(即LL(D)分别对α、u和∑求偏导 ),对参数进行迭代更新。
|
|
|
|
|
|
-
|
|
|
+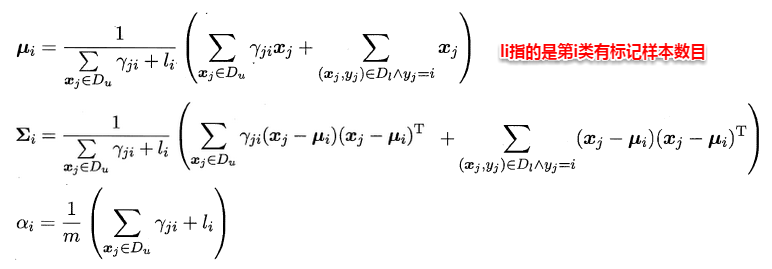
|
|
|
|
|
|
当参数迭代更新收敛后,对于待预测样本x,便可以像贝叶斯分类器那样计算出样本属于每个类簇的后验概率,接着找出概率最大的即可:
|
|
|
|
|
|
-
|
|
|
+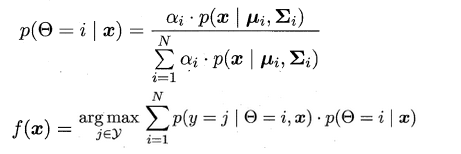
|
|
|
|
|
|
可以看出:基于生成式模型的方法十分依赖于对潜在数据分布的假设,即假设的分布要能和真实分布相吻合,否则利用未标记的样本数据反倒会在错误的道路上渐行渐远,从而降低学习器的泛化性能。因此,**此类方法要求极强的领域知识和掐指观天的本领**。
|
|
|
|
|
|
@@ -38,8 +38,9 @@
|
|
|
|
|
|
监督学习中的SVM试图找到一个划分超平面,使得两侧支持向量之间的间隔最大,即“**最大划分间隔**”思想。对于半监督学习,S3VM则考虑超平面需穿过数据低密度的区域。TSVM是半监督支持向量机中的最著名代表,其核心思想是:尝试为未标记样本找到合适的标记指派,使得超平面划分后的间隔最大化。TSVM采用局部搜索的策略来进行迭代求解,即首先使用有标记样本集训练出一个初始SVM,接着使用该学习器对未标记样本进行打标,这样所有样本都有了标记,并基于这些有标记的样本重新训练SVM,之后再寻找易出错样本不断调整。整个算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
- 
|
|
|
+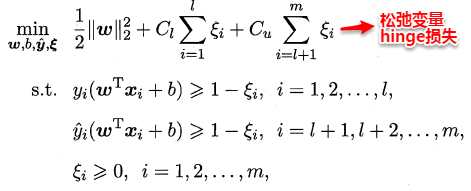
|
|
|
+
|
|
|
+
|
|
|
|
|
|
##**14.3 基于分歧的方法**
|
|
|
|
|
|
@@ -50,8 +51,8 @@
|
|
|
|
|
|
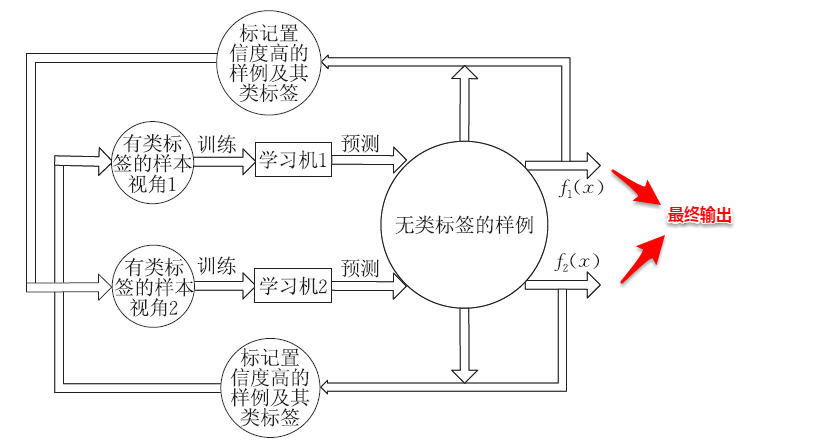
协同训练正是很好地利用了多视图数据的“**相容互补性**”,其基本的思想是:首先基于有标记样本数据在每个视图上都训练一个初始分类器,然后让每个分类器去挑选分类置信度最高的样本并赋予标记,并将带有伪标记的样本数据传给另一个分类器去学习,从而**你依我侬/共同进步**。
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+
|
|
|
+
|
|
|
|
|
|
|
|
|
##**14.4 半监督聚类**
|
|
|
@@ -63,12 +64,11 @@
|
|
|
|
|
|
下面主要介绍两种基于半监督的K-Means聚类算法:第一种是数据集包含一些必连与勿连关系,另外一种则是包含少量带有标记的样本。两种算法的基本思想都十分的简单:对于带有约束关系的k-均值算法,在迭代过程中对每个样本划分类簇时,需要**检测当前划分是否满足约束关系**,若不满足则会将该样本划分到距离次小对应的类簇中,再继续检测是否满足约束关系,直到完成所有样本的划分。算法流程如下图所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
对于带有少量标记样本的k-均值算法,则可以**利用这些有标记样本进行类中心的指定,同时在对样本进行划分时,不需要改变这些有标记样本的簇隶属关系**,直接将其划分到对应类簇即可。算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
在此,半监督学习就介绍完毕~十分有趣的是:半监督学习将前面许多知识模块联系在了一起,足以体现了作者编排的用心。结合本篇的新知识再来回想之前自己做过的一些研究,发现还是蹚了一些浑水,也许越是觉得过去的自己傻,越就是好的兆头吧~
|
|
|
|
|
|
-
|