|
|
@@ -8,7 +8,7 @@
|
|
|
|
|
|
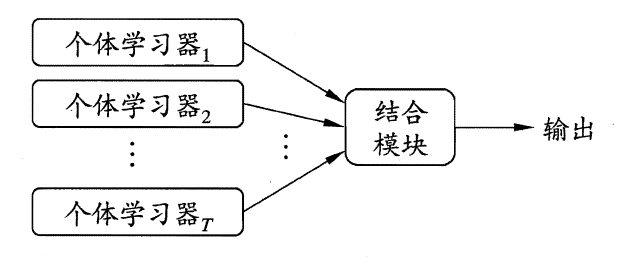
集成学习的基本结构为:先产生一组个体学习器,再使用某种策略将它们结合在一起。集成模型如下图所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
在上图的集成模型中,若个体学习器都属于同一类别,例如都是决策树或都是神经网络,则称该集成为同质的(homogeneous);若个体学习器包含多种类型的学习算法,例如既有决策树又有神经网络,则称该集成为异质的(heterogenous)。
|
|
|
|
|
|
@@ -19,11 +19,11 @@
|
|
|
|
|
|
上面我们已经提到要让集成起来的泛化性能比单个学习器都要好,虽说团结力量大但也有木桶短板理论调皮捣蛋,那如何做到呢?这就引出了集成学习的两个重要概念:**准确性**和**多样性**(diversity)。准确性指的是个体学习器不能太差,要有一定的准确度;多样性则是个体学习器之间的输出要具有差异性。通过下面的这三个例子可以很容易看出这一点,准确度较高,差异度也较高,可以较好地提升集成性能。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
现在考虑二分类的简单情形,假设基分类器之间相互独立(能提供较高的差异度),且错误率相等为 ε,则可以将集成器的预测看做一个伯努利实验,易知当所有基分类器中不足一半预测正确的情况下,集成器预测错误,所以集成器的错误率可以计算为:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
此时,集成器错误率随着基分类器的个数的增加呈指数下降,但前提是基分类器之间相互独立,在实际情形中显然是不可能的,假设训练有A和B两个分类器,对于某个测试样本,显然满足:P(A=1 | B=1)> P(A=1),因为A和B为了解决相同的问题而训练,因此在预测新样本时存在着很大的联系。因此,**个体学习器的“准确性”和“差异性”本身就是一对矛盾的变量**,准确性高意味着牺牲多样性,所以产生“**好而不同**”的个体学习器正是集成学习研究的核心。现阶段有三种主流的集成学习方法:Boosting、Bagging以及随机森林(Random Forest),接下来将进行逐一介绍。
|
|
|
|
|
|
@@ -35,11 +35,11 @@ Boosting族算法最著名、使用最为广泛的就是AdaBoost,因此下面
|
|
|
|
|
|
定义基学习器的集成为加权结合,则有:
|
|
|
|
|
|
-
|
|
|
+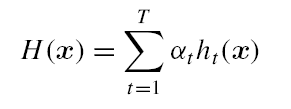
|
|
|
|
|
|
AdaBoost算法的指数损失函数定义为:
|
|
|
|
|
|
-
|
|
|
+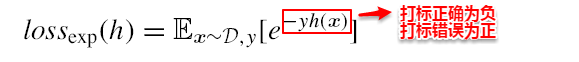
|
|
|
|
|
|
具体说来,整个Adaboost 迭代算法分为3步:
|
|
|
|
|
|
@@ -49,7 +49,7 @@ AdaBoost算法的指数损失函数定义为:
|
|
|
|
|
|
整个AdaBoost的算法流程如下所示:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
可以看出:**AdaBoost的核心步骤就是计算基学习器权重和样本权重分布**,那为何是上述的计算公式呢?这就涉及到了我们之前为什么说大部分带参机器学习算法只是改变了损失函数,就是因为**大部分模型的参数都是通过最优化损失函数(可能还加个规则项)而计算(梯度下降,坐标下降等)得到**,这里正是通过最优化指数损失函数从而得到这两个参数的计算公式,具体的推导过程此处不进行展开。
|
|
|
|
|
|
@@ -71,11 +71,11 @@ Boosting算法要求基学习器能对特定分布的数据进行学习,即每
|
|
|
|
|
|
Bagging是一种并行式的集成学习方法,即基学习器的训练之间没有前后顺序可以同时进行,Bagging使用“有放回”采样的方式选取训练集,对于包含m个样本的训练集,进行m次有放回的随机采样操作,从而得到m个样本的采样集,这样训练集中有接近36.8%的样本没有被采到。按照相同的方式重复进行,我们就可以采集到T个包含m个样本的数据集,从而训练出T个基学习器,最终对这T个基学习器的输出进行结合。
|
|
|
|
|
|
-
|
|
|
+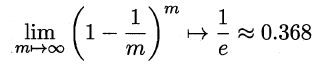
|
|
|
|
|
|
Bagging算法的流程如下所示:
|
|
|
|
|
|
-
|
|
|
+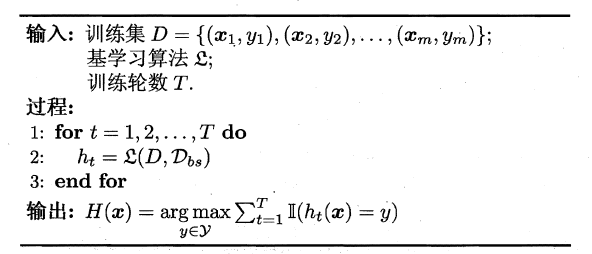
|
|
|
|
|
|
可以看出Bagging主要通过**样本的扰动**来增加基学习器之间的多样性,因此Bagging的基学习器应为那些对训练集十分敏感的不稳定学习算法,例如:神经网络与决策树等。从偏差-方差分解来看,Bagging算法主要关注于降低方差,即通过多次重复训练提高稳定性。不同于AdaBoost的是,Bagging可以十分简单地移植到多分类、回归等问题。总的说起来则是:**AdaBoost关注于降低偏差,而Bagging关注于降低方差。**
|
|
|
|
|
|
@@ -85,7 +85,7 @@ Bagging算法的流程如下所示:
|
|
|
|
|
|
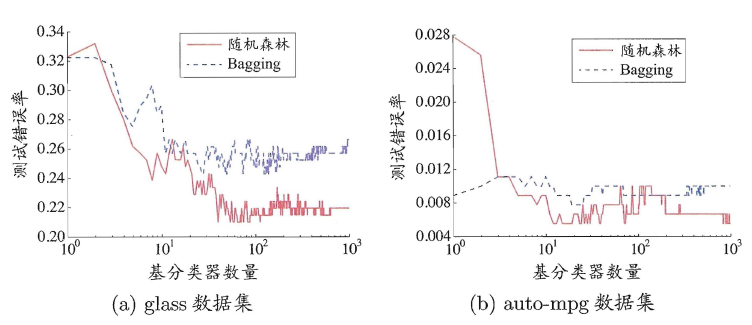
这样随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,从而进一步提升了基学习器之间的差异度。相比决策树的Bagging集成,随机森林的起始性能较差(由于属性扰动,基决策树的准确度有所下降),但随着基学习器数目的增多,随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划分属性,随机森林只在属性集的一个子集中选择划分属性,因此训练效率更高。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**9.4 结合策略**
|
|
|
|
|
|
@@ -93,20 +93,23 @@ Bagging算法的流程如下所示:
|
|
|
|
|
|
###**9.4.1 平均法(回归问题)**
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+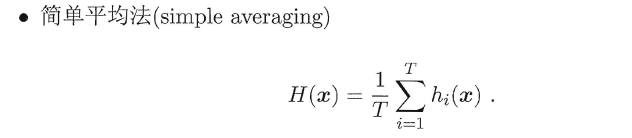
|
|
|
+
|
|
|
+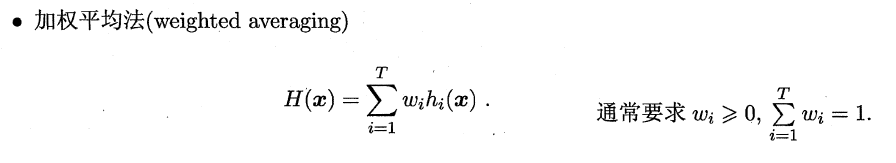
|
|
|
|
|
|
易知简单平均法是加权平均法的一种特例,加权平均法可以认为是集成学习研究的基本出发点。由于各个基学习器的权值在训练中得出,**一般而言,在个体学习器性能相差较大时宜使用加权平均法,在个体学习器性能相差较小时宜使用简单平均法**。
|
|
|
|
|
|
###**9.4.2 投票法(分类问题)**
|
|
|
|
|
|
-
|
|
|
-
|
|
|
-
|
|
|
+
|
|
|
+
|
|
|
+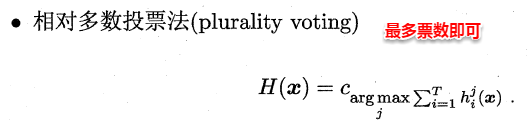
|
|
|
+
|
|
|
+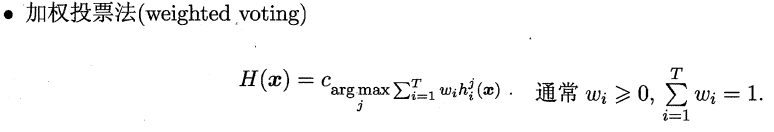
|
|
|
|
|
|
绝对多数投票法(majority voting)提供了拒绝选项,这在可靠性要求很高的学习任务中是一个很好的机制。同时,对于分类任务,各个基学习器的输出值有两种类型,分别为类标记和类概率。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
一些在产生类别标记的同时也生成置信度的学习器,置信度可转化为类概率使用,**一般基于类概率进行结合往往比基于类标记进行结合的效果更好**,需要注意的是对于异质集成,其类概率不能直接进行比较,此时需要将类概率转化为类标记输出,然后再投票。
|
|
|
|
|
|
@@ -115,7 +118,7 @@ Bagging算法的流程如下所示:
|
|
|
|
|
|
学习法是一种更高级的结合策略,即学习出一种“投票”的学习器,Stacking是学习法的典型代表。Stacking的基本思想是:首先训练出T个基学习器,对于一个样本它们会产生T个输出,将这T个基学习器的输出与该样本的真实标记作为新的样本,m个样本就会产生一个m*T的样本集,来训练一个新的“投票”学习器。投票学习器的输入属性与学习算法对Stacking集成的泛化性能有很大的影响,书中已经提到:**投票学习器采用类概率作为输入属性,选用多响应线性回归(MLR)一般会产生较好的效果**。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**9.5 多样性(diversity)**
|
|
|
|