|
|
@@ -26,7 +26,7 @@
|
|
|
|
|
|
对于特征子集的评价,书中给出了一些想法及基于信息熵的方法。假设数据集的属性皆为离散属性,这样给定一个特征子集,便可以通过这个特征子集的取值将数据集合划分为V个子集。例如:A1={男,女},A2={本科,硕士}就可以将原数据集划分为2*2=4个子集,其中每个子集的取值完全相同。这时我们就可以像决策树选择划分属性那样,通过计算信息增益来评价该属性子集的好坏。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
此时,信息增益越大表示该属性子集包含有助于分类的特征越多,使用上述这种**子集搜索与子集评价相结合的机制,便可以得到特征选择方法**。值得一提的是若将前向搜索策略与信息增益结合在一起,与前面我们讲到的ID3决策树十分地相似。事实上,决策树也可以用于特征选择,树节点划分属性组成的集合便是选择出的特征子集。
|
|
|
|
|
|
@@ -37,13 +37,13 @@
|
|
|
|
|
|
易知Relief算法的核心在于如何计算出该相关统计量。对于数据集中的每个样例xi,Relief首先找出与xi同类别的最近邻与不同类别的最近邻,分别称为**猜中近邻(near-hit)**与**猜错近邻(near-miss)**,接着便可以分别计算出相关统计量中的每个分量。对于j分量:
|
|
|
|
|
|
-
|
|
|
+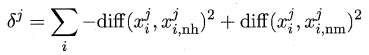
|
|
|
|
|
|
直观上理解:对于猜中近邻,两者j属性的距离越小越好,对于猜错近邻,j属性距离越大越好。更一般地,若xi为离散属性,diff取海明距离,即相同取0,不同取1;若xi为连续属性,则diff为曼哈顿距离,即取差的绝对值。分别计算每个分量,最终取平均便得到了整个相关统计量。
|
|
|
|
|
|
标准的Relief算法只用于二分类问题,后续产生的拓展变体Relief-F则解决了多分类问题。对于j分量,新的计算公式如下:
|
|
|
|
|
|
-
|
|
|
+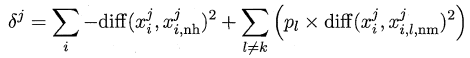
|
|
|
|
|
|
其中pl表示第l类样本在数据集中所占的比例,易知两者的不同之处在于:**标准Relief 只有一个猜错近邻,而Relief-F有多个猜错近邻**。
|
|
|
|
|
|
@@ -60,13 +60,13 @@
|
|
|
|
|
|
LVW算法的具体流程如下所示,其中比较特别的是停止条件参数T的设置,即在每一轮寻找最优特征子集的过程中,若随机T次仍没找到,算法就会停止,从而保证了算法运行时间的可行性。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**12.4 嵌入式选择与正则化**
|
|
|
|
|
|
前面提到了的两种特征选择方法:**过滤式中特征选择与后续学习器完全分离,包裹式则是使用学习器作为特征选择的评价准则;嵌入式是一种将特征选择与学习器训练完全融合的特征选择方法,即将特征选择融入学习器的优化过程中**。在之前《经验风险与结构风险》中已经提到:经验风险指的是模型与训练数据的契合度,结构风险则是模型的复杂程度,机器学习的核心任务就是:**在模型简单的基础上保证模型的契合度**。例如:岭回归就是加上了L2范数的最小二乘法,有效地解决了奇异矩阵、过拟合等诸多问题,下面的嵌入式特征选择则是在损失函数后加上了L1范数。
|
|
|
|
|
|
-
|
|
|
+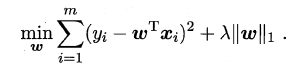
|
|
|
|
|
|
L1范数美名又约**Lasso Regularization**,指的是向量中每个元素的绝对值之和,这样在优化目标函数的过程中,就会使得w尽可能地小,在一定程度上起到了防止过拟合的作用,同时与L2范数(Ridge Regularization )不同的是,L1范数会使得部分w变为0, 从而达到了特征选择的效果。
|
|
|
|
|
|
@@ -74,12 +74,13 @@ L1范数美名又约**Lasso Regularization**,指的是向量中每个元素的
|
|
|
|
|
|
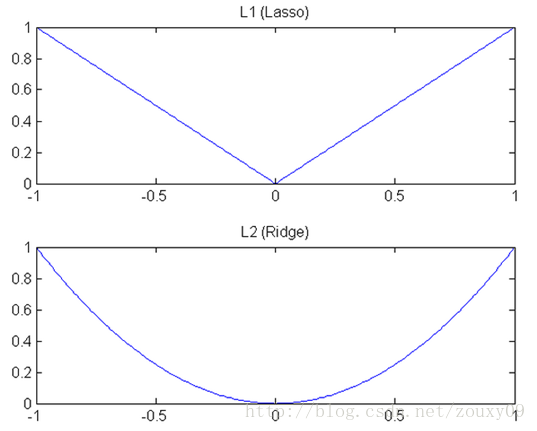
(1)**下降速度**:L1范数按照绝对值函数来下降,L2范数按照二次函数来下降。因此在0附近,L1范数的下降速度大于L2范数,故L1范数能很快地下降到0,而L2范数在0附近的下降速度非常慢,因此较大可能收敛在0的附近。
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
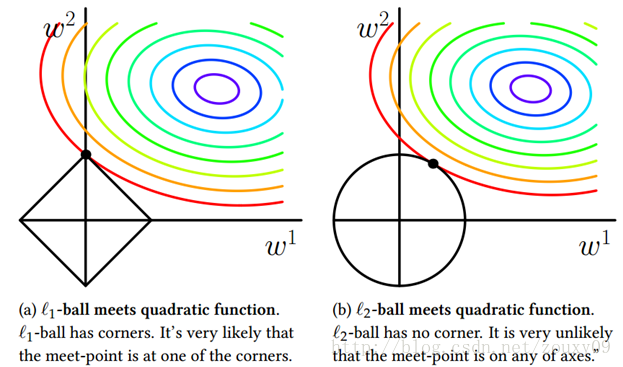
(2)**空间限制**:L1范数与L2范数都试图在最小化损失函数的同时,让权值W也尽可能地小。我们可以将原优化问题看做为下面的问题,即让后面的规则则都小于某个阈值。这样从图中可以看出:L1范数相比L2范数更容易得到稀疏解。
|
|
|
|
|
|
-
|
|
|
-
|
|
|
+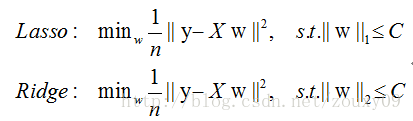
|
|
|
+
|
|
|
+
|
|
|
|
|
|
##**12.5 稀疏表示与字典学习**
|
|
|
|
|
|
@@ -87,13 +88,13 @@ L1范数美名又约**Lasso Regularization**,指的是向量中每个元素的
|
|
|
|
|
|
给定一个数据集,字典学习/稀疏编码指的便是通过一个字典将原数据转化为稀疏表示,因此最终的目标就是求得字典矩阵B及稀疏表示α,书中使用变量交替优化的策略能较好地求得解,深感陷进去短时间无法自拔,故先不进行深入...
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
##**12.6 压缩感知**
|
|
|
|
|
|
压缩感知在前些年也是风风火火,与特征选择、稀疏表示不同的是:它关注的是通过欠采样信息来恢复全部信息。在实际问题中,为了方便传输和存储,我们一般将数字信息进行压缩,这样就有可能损失部分信息,如何根据已有的信息来重构出全部信号,这便是压缩感知的来历,压缩感知的前提是已知的信息具有稀疏表示。下面是关于压缩感知的一些背景:
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
在此,特征选择与稀疏学习就介绍完毕。在很多实际情形中,选了好的特征比选了好的模型更为重要,这也是为什么厉害的大牛能够很快地得出一些结论的原因,谓:吾昨晚夜观天象,星象云是否吃货乃无用也~
|
|
|
|